Гравитация внутри полой сферы

@Элд Хасп · Регистрация: 21.04.2018

Студворк — интернет-сервис помощи студентам

Физикой сильно не увлекаюсь - так любопытничаю.
Случайно прочитал в статье, что сила тяжести внутри сферы уравновешена и все тела находятся в состоянии невесомости.
И доказано это ещё Ньютоном.

Мне как-то показалось это неправдоподобным.
Поискал ещё - не сказать, что много нашёл. Но всюду утверждается так же.
Вопрос - я не знаю физику или я не знаю где искать?

@Почтальон · 14.01.2020, 12:47

Для силы тяжести - нужна масса, так что гравитация внутри полой сферы будет

@SSC · 14.01.2020, 12:51

Сообщение от Элд Хасп

я не знаю где искать?

Посмотрите материалы по запросу в google
"сила тяжести в центре земли"

@Элд Хасп · 14.01.2020, 13:25 **[ТС]**

Сообщение от SSC

Посмотрите материалы по запросу в google
"сила тяжести в центре земли"

Ну, блин, снисходительнее всё таки... Или думаете я даже погуглить сам не в состоянии?

Вот ссылки где затрагивается тема точки внутри полой сферы (не внутри ЗЕМЛИ!)
https://elementy.ru/posters/gravity/6

То есть сфера вообще не действует на точечную массу, расположенную внутри нее, в каком бы месте эта точечная масса ни находилась (совершенно необязательно, чтобы она находилась в центре сферы!).

http://interesnik.com/zabluzhd... enyaetsya/

Лишним подтверждением этому факту служит строгое математическое доказательство отсутствия притяжения внутри сферы.

http://www.geokniga.org/sites/... 226/15.pdf

Отсюда вывод: материальная точка, помещенная внутри полой сферы, этой сферой не притягивается

И так же всюду где попадался мне этот вопрос.
Но не смотря на это мне кажется это неправдоподобным.
Отсюда и возник мой вопрос.

Сообщение от Почтальон

Для силы тяжести - нужна масса, так что гравитация внутри полой сферы будет

Я тоже так думаю. Но почему-то всюду где нашёл утверждается противоположное.

@SSC · 14.01.2020, 14:02

Сообщение от Элд Хасп

То есть сфера вообще не действует на точечную массу, расположенную внутри нее,

Методологически это неверно.
Если разбить сферу на N частей, то каждая часть будет притягивать точечную массу. Поэтому и вся сфера будет создавать силу притяжения. Однако если точечная масса расположена в центре сферы, то равнодействующая сила от всех сил притяжения к N частям сферы будет равна нулю.
Следовательно гравитация на точечную массу в центре сферы будет действовать (уже в силу того, что что объект обладает массой), однако гравитационная сила притяжения этой точечной массы к сфере равна нулю, и можно считать что данный объект по отношению к сфере находится в "невесомости".
Это как в электростатике. Например есть два положительных равных заряда на некотором расстоянии. Точно посередине помещаем малый пробный заряд. Силы Кулона будут действовать на пробный заряд. Электростатическое поле будет. Но равнодействующая сил Кулона будет равна нулю.

@Ygg · 14.01.2020, 14:04

Сообщение от Элд Хасп

Но не смотря на это мне кажется это неправдоподобным.

Почему же, всё вполне логично. Силы притяжения от всех точек сферы внутри данной сферы полностью уравновешены. Снаружи сферы результирающая сил от всех точек данной сферы аналогична силе от равной массы помещённой в цент. Что именно вам кажется неправдоподобным?

@Элд Хасп · 14.01.2020, 14:56 **[ТС]**

Сообщение от SSC

Методологически это неверно.

Я ещё раз уточняю.
Я не интересуюсь за ЦЕНТР сферы.
Речь идёт за любое место внутри сферы.

Прочитайте статьи из которых я привёл ссылки.

Добавлено через 1 минуту

Сообщение от Ygg

Что именно вам кажется неправдоподобным?

Именно резкий ступенчатый обрыв силы притяжения.
На R+0 сила есть и она значительная, а на R-0 сразу ноль.

То есть это на самом деле так и мои сомнения необоснованны?

Добавлено через 7 минут
Ygg, пока без расчётов чисто логически.

Сфера размером в километр. Точка внутри сферы на расстоянии 1 мм
Мысленно разрезаем сферу плоскостью проходящей через точку и перпендикулярную прямой соединяющей точку с центром сферы.

По принципу симметрии обе части сферы будут тянуть точку строго вдоль прямой от точки к сфере, но в разных направлениях.
И что сила притяжения "отрезанной крышки" размером в метр-два будет равна силе притяжения всей остальной сферы?

iifat · 14.01.2020, 15:33

Сообщение от SSC

если точечная масса расположена в центре сферы, то равнодействующая сила от всех сил притяжения к N частям сферы будет равна нулю

В любой точке сферы. Не только в центре.

Сообщение от Элд Хасп

И что сила притяжения "отрезанной крышки" размером в метр-два будет равна силе притяжения всей остальной сферы?

Напоминаю: кроме массы в уравнение Ньютона входит эр в квадрате.

@Ygg · 14.01.2020, 15:42

Сообщение от Элд Хасп

И что сила притяжения "отрезанной крышки" размером в метр-два будет равна силе притяжения всей остальной сферы?

Да. Всё волшебство в квадрате расстояния в знаменателе формулы для силы притяжения. "Крышка" гораздо ближе, но меньше. Оставшаяся часть больше, но дальше. В результате силы от таких неравных частей сферы уравновешиваются. Строгое доказательство через интегралы непосильно моему разумению, но я доверяю математикам в этом вопросе

В первой вашей ссылке есть описание уравновешивания через сектора. Оно приблизительно, но более-менее наглядно. Ещё где-то встречал чуть более подробное описание тройного интегрирования вдоль оси симметрии: точка, кольцо, сфера. Не помню где, но вроде там чуть понятнее для меня было, по сравнению с вашей третьей ссылкой. Выкладки для случая внутри сферы и снаружи чем-то перекликаются. Можно поискать какой-нибудь материал для точки снаружи сферы.

@Элд Хасп · 14.01.2020, 16:12 **[ТС]**

iifat, Ygg, R^2 не спасёт, по моему.

Если есть возможность и желание давайте разложим по полочкам.

Законы Ньютона напрямую задают силу притяжения между точками.

1. Для начала рассмотрим систему из трёх точек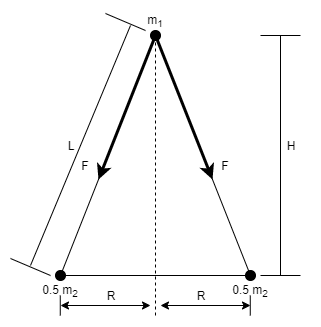

m1 – точка
m2 – две равные точки общей массы
L – расстояние межу точками
F – сила притяжения
R - расстояние от перпендикуляра
H – высота перпендикуляра

(1): $https://www.cyberforum.ru/cgi-bin/latex.cgi?L=\sqrt{{R}^{2}+{H}^{2}}$

(2): $https://www.cyberforum.ru/cgi-bin/latex.cgi?F=G*\frac{0.5*{m}_{1}*{m}_{2}}{{L}^{2}}$

(3): $https://www.cyberforum.ru/cgi-bin/latex.cgi?f=\vec{{F}_{1}} + \vec{{F}_{2}} = 2*F*\frac{H}{L}=G\frac{{m}_{1}{m}_{2}H}{{L}^{3}}$

2. Притяжение точки к кругу.
Круг состоит из точек, равноудалённых от центра.
Если точка лежит на прямой проходящей через центр круга и перпендикулярной плоскости круга, то все точки круга так же равноудалены от исходной точки.
Раз все точки равноудалены от исходной точки, то притяжение между кругом и точкой определяется также по формуле 3, где m2 – это масса круга

Рассуждение верные? Ошибки нигде нет?

@Ygg · 14.01.2020, 16:26

Сообщение от Элд Хасп

Рассуждение верные? Ошибки нигде нет?

Вроде верные пока, но iifat и SSC лучше меня в математике разбираются, так что лучше у них спрашивать

@Элд Хасп · 14.01.2020, 16:38 **[ТС]**

Сообщение от Ygg

iifat и SSC лучше меня в математике разбираются, так что лучше у них спрашивать

Будем ждать.

iifat · 14.01.2020, 16:41

Сообщение от Элд Хасп

Ошибки нигде нет?

Похоже на то.

@Элд Хасп · 14.01.2020, 17:46 **[ТС]**

Сообщение от iifat

Похоже на то.

Сфера состоит из кругов перпендикулярных этой плоскости. Так как притяжение к кругу равносильно притяжению к двум его противоположным точкам с общей массой раной массе круга, то притяжение каждого круга равно точкам его пересечения с плоскостью.
Все точки пересечения кругов с плоскостью тоже образуют круг общей массой равной массе круга.
Масса каждой окружности пропорциональна длине его окружности и, следовательно, его радиусу.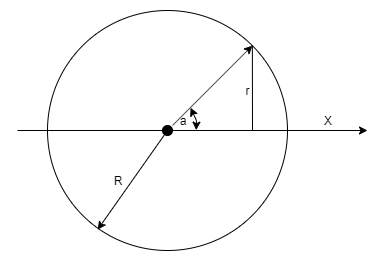

R – Радиус сферы
a – у=Угол функции
r – Радиус круга функции
X – Ось Абсцисс

Длина окружности (4): $https://www.cyberforum.ru/cgi-bin/latex.cgi?L=2\pi {r}^{2}$

Радиус окружности (5): $https://www.cyberforum.ru/cgi-bin/latex.cgi?r=R*sin(\alpha )$

Масса окружности (6): $https://www.cyberforum.ru/cgi-bin/latex.cgi?m=L*\rho=2\pi\rho{r}^{2}=2\pi\rho*{R}^{2}*{sin}^{2}(\alpha )$ , где ρ – коэффициент линейной плотности

Общая масса сферы равна интегралу от масс кругов:
(7): $https://www.cyberforum.ru/cgi-bin/latex.cgi?M=\int_{0}^{\pi}2\pi \rho{R}^{2}{sin}^{2}(\alpha )d\alpha = 2\pi\rho {R}^{2}\left(\frac{\alpha }{2}-\frac{sin2\alpha }{4}\right)0...\pi$
не нашёл как в LATEX указывать диапазон написал 0...pi
Расчёт по диапазону $https://www.cyberforum.ru/cgi-bin/latex.cgi?M=\rho *{R}^{2}*{\pi }^{2}$

Отсюда приведённая плотность (8): $https://www.cyberforum.ru/cgi-bin/latex.cgi?\rho =\frac{M}{{\pi }^{2}*{R}^{2}}$

Пока ошибок нет?

@Ygg · 14.01.2020, 19:35

Сообщение от Элд Хасп

Пока ошибок нет?

В длине окружности (4) радиус без квадрата, вроде бы.

@Элд Хасп · 14.01.2020, 20:52 **[ТС]**

Сообщение от Ygg

В длине окружности (4) радиус без квадрата, вроде бы.

Точно!
Корректирую

(4) - $https://www.cyberforum.ru/cgi-bin/latex.cgi?L=2\pi R$

(5) - без изменений

(6) - $https://www.cyberforum.ru/cgi-bin/latex.cgi?m=L*\rho =2\pi \rho r=2\pi \rho R sin(\alpha )$

(7) - $https://www.cyberforum.ru/cgi-bin/latex.cgi?M = \int_{0}^{\pi }2\pi \rho R *sin(\alpha ) d\alpha = -2\pi \rho R *cos(\alpha ) \left|\frac{\pi }{0}= -2\pi \rho R *\left(-1-1 \right)= 4\pi \rho R$

Здорово! Конкретно проще получилось!

(8) - $https://www.cyberforum.ru/cgi-bin/latex.cgi?\rho = \frac{M}{4\pi R}$

Так вроде правильно.

Теперь надо перевести всё это в силу притяжения.

@Элд Хасп · 14.01.2020, 23:25 **[ТС]**

Рассмотрим притяжение точки к одной из точек окружности, представляющего радиальную проекцию сферы на плоскость.
Ранее мы уже выяснили, что физически притяжение точки к сфере равносильно к притяжению к этой проекции не зависимо от взаимных расположений точки и сферы.
В том числе точка может находиться и внутри сферы.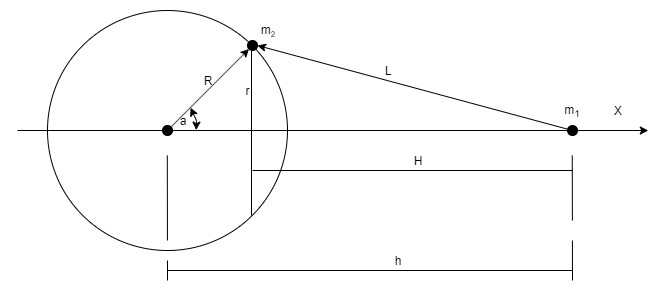

Сила притяжении точки m₁ к точке m₂, являющейся проекцией окружности из (3):

(3): $https://www.cyberforum.ru/cgi-bin/latex.cgi?f=G\frac{{m}_{1}{m}_{2}H}{{L}^{3}}$

Подставляем переменные:

Масса окружности (9): $https://www.cyberforum.ru/cgi-bin/latex.cgi?{m}_{2}=2\pi \rho R*sin(\alpha )= 2\pi \frac{M}{4\pi R}R*sin(\alpha )=\frac{1}{2}M*sin(\alpha )$

Расстояние от точки до плоскости окружности (10): $https://www.cyberforum.ru/cgi-bin/latex.cgi?H=h-R*cos(\alpha )$

Расстояние от точки до точки окружности (11):

$https://www.cyberforum.ru/cgi-bin/latex.cgi?L=\sqrt{\left({H}^{2}+{\left(R*sin(\alpha ) \right)}^{2} \right)}=\sqrt{{h}^{2}-2hR*cos(\alpha )+{R}^{2}{cos}^{2}(\alpha )+{R}^{2}{sin}^{2}(\alpha )}=\sqrt{{h}^{2}-2hR*cos(\alpha )+{R}^{2}}$

Общая формула притяжения между точкой и окружностью сферы (11):

$https://www.cyberforum.ru/cgi-bin/latex.cgi?f=G*\frac{{m}_{1}M}{2}*\frac{sin(\alpha )*\left(h-cos(\alpha ) \right)}{{\left({h}^{2}-2hR*cos(\alpha ) +{R}^{2}\right)}^{1.5}}$

Общую силу притяжения между точкой и сферой даст интеграл этой функции в диапазоне от 0 до π

Интегрирование в общем виде пока оставим - к этому я ещё морально не готов.
Сделаем оценку при h=0 и h>>R

Для h=0 (12): $https://www.cyberforum.ru/cgi-bin/latex.cgi?{f}_{0}=\int_{0}^{\pi }G*\frac{{m}_{1}M}{2}*\frac{-sin(\alpha )cos(\alpha )}{{R}^{3}}d\alpha =-G*\frac{{m}_{1}M}{2{R}^{3}}*\frac{1}{4}cos(2\alpha )\left|\frac{\pi }{0}=0$

Для h>>R (13): $https://www.cyberforum.ru/cgi-bin/latex.cgi?{f}_{rr}=\int_{0}^{\pi }G*\frac{{m}_{1}M}{2}*\frac{sin(\alpha )h}{{h}^{3}}d\alpha =-G*\frac{{m}_{1}M}{2{h}^{2}}*cos(\alpha )\left|\frac{\pi }{0}=G*\frac{{m}_{1}M}{2{h}^{2}}$

Получаем , что в центре сферы притяжение равно нулю, а на большом удаления обратно пропорционально квадрату расстояния.
Для крайних значений ответ верный.

Что ещё можно сказать об этой (11) функции? Она непрерывная, дифференцируема и интегрируема во всём числовом диапазоне.
Никаких скачков ступенек в ней быть не может.

С интегралами дружу слабо. Надо попросить кого-нибудь чтобы помог получить интеграл в общем виде.

Пока же прошу проверить остальную часть выводов.

iifat · 15.01.2020, 00:05

Пока навскидку, некогда. Попозже почту внимательнее.

Сообщение от Элд Хасп

Что ещё можно сказать об этой функции. Она непрерывная, дифференцируема и интегрируема во всём числовом диапазоне.
Никаких скачков ступенек в ней быть не может

Какая именно функция? $https://www.cyberforum.ru/cgi-bin/latex.cgi?f_{rr}(h)$ ? А в нуле она тоже дифференцируема? А ничего, что в нуле она обращается в бесконечность, а у вас вдруг ра вна нулю?

@Элд Хасп · 15.01.2020, 00:41 **[ТС]**

iifat, разве при h=0 (формула 12) есть какие-то проблемы с дифференцированием?
Где она там в бесконечность обращается?

Или я не понял о чём вы?

Добавлено через 2 минуты
Основная же формула это 11-я.
А 13-я это приближение при h>>R.
Здесь h априори не нуль.

iifat · 15.01.2020, 08:11

11-я так 11-я. Кстати говоря, в числителе там $https://www.cyberforum.ru/cgi-bin/latex.cgi?h-R\cos\alpha$

Новые блоги и статьи Все статьи Все блоги /
SDL3 для Web (WebAssembly): Реализация движения на Box2D v3 - трение и коллизии с повёрнутыми стенами 8Observer8 20.02.2026 Содержание блога Box2D позволяет легко создать главного героя, который не проходит сквозь стены и перемещается с заданным трением о препятствия, которые можно располагать под углом, как верхнее. . .	Конвертировать закладки radiotray-ng в m3u-плейлист damix 19.02.2026 Это можно сделать скриптом для PowerShell. Использование . \СonvertRadiotrayToM3U. ps1 <path_to_bookmarks. json> Рядом с файлом bookmarks. json появится файл bookmarks. m3u с результатом. # Check if. . .	Семь CDC на одном интерфейсе: 5 U[S]ARTов, 1 CAN и 1 SSI Eddy_Em 18.02.2026 Постепенно допиливаю свою "многоинтерфейсную плату". Выглядит вот так: https:/ / www. cyberforum. ru/ blog_attachment. php?attachmentid=11617&stc=1&d=1771445347 Основана на STM32F303RBT6. На борту пять. . .	Камера Toupcam IUA500KMA Eddy_Em 12.02.2026 Т. к. у всяких "хикроботов" слишком уж мелкий пиксель, для подсмотра в ESPriF они вообще плохо годятся: уже 14 величину можно рассмотреть еле-еле лишь на экспозициях под 3 секунды (а то и больше),. . .
И ясному Солнцу zbw 12.02.2026 И ясному Солнцу, и светлой Луне. В мире покоя нет и люди не могут жить в тишине. А жить им немного лет.	«Знание-Сила» zbw 12.02.2026 «Знание-Сила» «Время-Деньги» «Деньги -Пуля»	SDL3 для Web (WebAssembly): Подключение Box2D v3, физика и отрисовка коллайдеров 8Observer8 12.02.2026 Содержание блога Box2D - это библиотека для 2D физики для анимаций и игр. С её помощью можно определять были ли коллизии между конкретными объектами и вызывать обработчики событий столкновения. . . .	SDL3 для Web (WebAssembly): Загрузка PNG с прозрачным фоном с помощью SDL_LoadPNG (без SDL3_image) 8Observer8 11.02.2026 Содержание блога Библиотека SDL3 содержит встроенные инструменты для базовой работы с изображениями - без использования библиотеки SDL3_image. Пошагово создадим проект для загрузки изображения. . .

@Элд Хасп Модератор 16130 / 11254 / 2888 Регистрация: 21.04.2018 Сообщений: 33,086 Записей в блоге: 2

	Гравитация внутри полой сферы 13.01.2020, 23:55. Показов 14838. Ответов 66 Метки нет (Все метки) Физикой сильно не увлекаюсь - так любопытничаю. Случайно прочитал в статье, что сила тяжести внутри сферы уравновешена и все тела находятся в состоянии невесомости. И доказано это ещё Ньютоном. Мне как-то показалось это неправдоподобным. Поискал ещё - не сказать, что много нашёл. Но всюду утверждается так же. Вопрос - я не знаю физику или я не знаю где искать? 0

@Почтальон управление сложностью 1693 / 1306 / 259 Регистрация: 22.03.2015 Сообщений: 7,545 Записей в блоге: 5
	14.01.2020, 12:47
	Для силы тяжести - нужна масса, так что гравитация внутри полой сферы будет 0

@Элд Хасп Модератор 16130 / 11254 / 2888 Регистрация: 21.04.2018 Сообщений: 33,086 Записей в блоге: 2
	14.01.2020, 16:12 [ТС]
	iifat, Ygg, R^2 не спасёт, по моему. Если есть возможность и желание давайте разложим по полочкам. Законы Ньютона напрямую задают силу притяжения между точками. 1. Для начала рассмотрим систему из трёх точек m1 – точка m2 – две равные точки общей массы L – расстояние межу точками F – сила притяжения R - расстояние от перпендикуляра H – высота перпендикуляра (1): $https://www.cyberforum.ru/cgi-bin/latex.cgi?L=\sqrt{{R}^{2}+{H}^{2}}$ (2): $https://www.cyberforum.ru/cgi-bin/latex.cgi?F=G\frac{0.5{m}_{1}{m}_{2}}{{L}^{2}}$ (3):* $https://www.cyberforum.ru/cgi-bin/latex.cgi?f=\vec{{F}_{1}} + \vec{{F}_{2}} = 2F\frac{H}{L}=G\frac{{m}_{1}{m}_{2}H}{{L}^{3}}$ 2. Притяжение точки к кругу. Круг состоит из точек, равноудалённых от центра. Если точка лежит на прямой проходящей через центр круга и перпендикулярной плоскости круга, то все точки круга так же равноудалены от исходной точки. Раз все точки равноудалены от исходной точки, то притяжение между кругом и точкой определяется также по формуле 3, где m2 – это масса круга Рассуждение верные? Ошибки нигде нет? 0

@Элд Хасп Модератор 16130 / 11254 / 2888 Регистрация: 21.04.2018 Сообщений: 33,086 Записей в блоге: 2
	14.01.2020, 23:25 [ТС]
	Рассмотрим притяжение точки к одной из точек окружности, представляющего радиальную проекцию сферы на плоскость. Ранее мы уже выяснили, что физически притяжение точки к сфере равносильно к притяжению к этой проекции не зависимо от взаимных расположений точки и сферы. В том числе точка может находиться и внутри сферы. Сила притяжении точки m₁ к точке m₂, являющейся проекцией окружности из (3): (3): $https://www.cyberforum.ru/cgi-bin/latex.cgi?f=G\frac{{m}_{1}{m}_{2}H}{{L}^{3}}$ Подставляем переменные: Масса окружности (9): $https://www.cyberforum.ru/cgi-bin/latex.cgi?{m}_{2}=2\pi \rho Rsin(\alpha )= 2\pi \frac{M}{4\pi R}Rsin(\alpha )=\frac{1}{2}Msin(\alpha )$ Расстояние от точки до плоскости окружности (10):* $https://www.cyberforum.ru/cgi-bin/latex.cgi?H=h-Rcos(\alpha )$ Расстояние от точки до точки окружности (11):* $https://www.cyberforum.ru/cgi-bin/latex.cgi?L=\sqrt{\left({H}^{2}+{\left(Rsin(\alpha ) \right)}^{2} \right)}=\sqrt{{h}^{2}-2hRcos(\alpha )+{R}^{2}{cos}^{2}(\alpha )+{R}^{2}{sin}^{2}(\alpha )}=\sqrt{{h}^{2}-2hRcos(\alpha )+{R}^{2}}$ Общая формула притяжения между точкой и окружностью сферы (11):* $https://www.cyberforum.ru/cgi-bin/latex.cgi?f=G\frac{{m}_{1}M}{2}\frac{sin(\alpha )\left(h-cos(\alpha ) \right)}{{\left({h}^{2}-2hRcos(\alpha ) +{R}^{2}\right)}^{1.5}}$ Общую силу притяжения между точкой и сферой даст интеграл этой функции в диапазоне от 0 до π Интегрирование в общем виде пока оставим - к этому я ещё морально не готов. Сделаем оценку при h=0 и h>>R Для h=0 (12): $https://www.cyberforum.ru/cgi-bin/latex.cgi?{f}_{0}=\int_{0}^{\pi }G\frac{{m}_{1}M}{2}\frac{-sin(\alpha )cos(\alpha )}{{R}^{3}}d\alpha =-G\frac{{m}_{1}M}{2{R}^{3}}\frac{1}{4}cos(2\alpha )\left\|\frac{\pi }{0}=0$ Для h>>R (13): $https://www.cyberforum.ru/cgi-bin/latex.cgi?{f}_{rr}=\int_{0}^{\pi }G\frac{{m}_{1}M}{2}\frac{sin(\alpha )h}{{h}^{3}}d\alpha =-G\frac{{m}_{1}M}{2{h}^{2}}cos(\alpha )\left\|\frac{\pi }{0}=G*\frac{{m}_{1}M}{2{h}^{2}}$ Получаем , что в центре сферы притяжение равно нулю, а на большом удаления обратно пропорционально квадрату расстояния. Для крайних значений ответ верный. Что ещё можно сказать об этой (11) функции? Она непрерывная, дифференцируема и интегрируема во всём числовом диапазоне. Никаких скачков ступенек в ней быть не может. С интегралами дружу слабо. Надо попросить кого-нибудь чтобы помог получить интеграл в общем виде. Пока же прошу проверить остальную часть выводов. 0

@Элд Хасп Модератор 16130 / 11254 / 2888 Регистрация: 21.04.2018 Сообщений: 33,086 Записей в блоге: 2
	15.01.2020, 00:41 [ТС]
	iifat, разве при h=0 (формула 12) есть какие-то проблемы с дифференцированием? Где она там в бесконечность обращается? Или я не понял о чём вы? Добавлено через 2 минуты Основная же формула это 11-я. А 13-я это приближение при h>>R. Здесь h априори не нуль. 0

iifat 2900 / 1934 / 209 Регистрация: 05.06.2011 Сообщений: 5,691
	15.01.2020, 08:11
	11-я так 11-я. Кстати говоря, в числителе там $https://www.cyberforum.ru/cgi-bin/latex.cgi?h-R\cos\alpha$ 1