Что может быть необычнее, чем применить законы квантовой механики для украшения новогодней елки? Пока другие развешивают обычные гирлянды, я решил объединить свою страсть к квантовым вычислениям с праздничными традициями. Результат эксперимента превзошел мои ожидания — елка, украшенная по законам квантовой физики, с использованием языков программирования Q# от Microsoft и Qiskit от IBM.
Представьте: каждое украшение на елке определяется не простым алгоритмом, а квантовыми эффектами суперпозиции, интерференции и запутаности. Вместо случайного распределения — паттерны, возникающие из фундаментальных квантовых феноменов. Классические вероятности заменяются квантовыми амплитудами, а декорации подчиняются принципам, которые когда-то казались Эйнштейну "жуткими действиями на расстоянии".
Когда физика встречается с праздником
За несколько лет работы с квантовыми технологиями я постоянно думал о том, как сделать эту сложную область более доступной и визуально понятной для обычных людей. И вот однажды, глядя на новогоднюю елку, меня озарило — а что если использовать квантовые алгоритмы для создания по-настоящему уникальных паттернов украшения? Обычно мы развешиваем игрушки, основываясь на эстетических предпочтениях или случайности. Но квантовый мир предлагает третий путь — узоры, рожденные фундаментальными законами природы на субатомном уровне. По сути, я захотел сделать видимыми те причудливые эффекты, которые обычно скрыты в глубинах квантовых процессоров.
Q# от Microsoft и Qiskit от IBM — два мощных инструмента для работы с квантовыми вычислениями. Q# привлекает меня своей строгой типизацией и интеграцией с экосистемой .NET, а Qiskit подкупает гибкостью Python и обширной библиотекой для визуализации результатов. И хотя изначально эти языки разрабатывались для решения сложных вычислительных задач, я понял, что могу "перенаправить" их для управления праздничными украшениями.
Суть проекта проста и одновременно сложна: создать программу, которая запускает квантовые схемы на симуляторе, интерпретирует результаты измерений и превращает их в конкретные типы и расположения украшений на виртуальной елке. Но вся красота в том, что паттерны украшений будут отражать реальные квантовые феномены! Для реализации этой идеи я разработал абстрактный слой, который позволяет запускать один и тот же код на обоих языках. Это важно, поскольку я хотел показать, как разные подходы к квантовым вычислениям могут порождать схожие визуальные результаты. Интерфейс моего симулятора предельно прост:
| Python | 1
2
3
4
5
| class QuantumSimulator(ABC):
@abstractmethod
def run_simulation(self, num_positions: int) -> str:
"""Запустить квантовую симуляцию и вернуть бинарную строку результатов"""
pass |
|
|00⟩ — красный шарик
|01⟩ — желтая звезда
|10⟩ — синий ромб
|11⟩ — пурпурная искрящаяся звезда
Когда я впервые запустил этот код, меня удивило, насколько неинтуитивными были узоры украшений. В отличе от псевдослучайных генераторов, которые часто создают довольно предсказуемые равномерные распределения, квантовые измерения давали интересные кластеры и корреляции между соседними позициями. И это имеет глубокий смысл — в коде мы специально используем квантовую запутаность между соседними позициями, заставляя украшения "чувствовать" друг друга на расстоянии.
Особено забавно наблюдать, как меняются узоры от запуска к запуску. Да, они случайны, но эта случайность фундаментально отличается от классической — она рождается из коллапса волновой функции при измерении. По сути, каждый раз, когда мы генерируем новую схему украшения, мы наблюдаем очередную реализацию квантовой вероятностной природы Вселенной, просто в очень упрощенной и праздничной форме.
Построить два окна на одном экране. В первом окне нарисуйте ёлку
Построить два окна на одном экране. В первом окне нарисуйте ёлку. Во втором окне напишите:... Рисую елку, проблема с полигонами
Рисую я вот эту елку.
Сделал вроде листву с помощью полигона, соед. начало и конец(откуда начал,... Нарисовать елку из треугольников
Нарисовать елку из треугольников.
Помогите пожалуйста на питоне.
Заранее спасибо! Нарисовать новогоднюю елку
доброго вам здоровья уважаемые! помогите пожалуйста нарисовать 2 не сложных обьекта
1 необходимо...
Под капотом квантовых огоньков
Чтобы по-настоящему понять, как работает наша квантовая елка, придется немного нырнуть в математические глубины. Не бойтесь, я постараюсь объяснить все максимально понятно, без лишних уравнений. Сначала поговорим о суперпозиции — краеугольном камне квантовых вычислений. В классическом мире бит может быть либо 0, либо 1. А квантовый бит (кубит) способен находиться в обоих состояниях одновременно! Математически это записывается как  где где 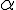 и и 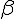 — комплексные амплитуды вероятности. — комплексные амплитуды вероятности.
В моей программе я использую вентиль Адамара (H-гейт), чтобы перевести каждый кубит в суперпозицию. Вот как это выглядит в Q#:
| Q# | 1
2
3
| for i in 0..qubitsNeeded-1 {
H(qubits[i]);
} |
|
| Python | 1
2
| for i in range(qubits_needed):
circuit.h(qr[i]) |
|
В следующем блоке кода я применяю фазовые вращения к кубитам. Вентиль S создает поворот на 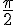 радиан, а вентиль T — на радиан, а вентиль T — на  радиан. Это не меняет вероятности измерения |0⟩ или |1⟩, но влияет на фазу волновой функции: радиан. Это не меняет вероятности измерения |0⟩ или |1⟩, но влияет на фазу волновой функции:
| Q# | 1
2
3
4
5
| for i in 0..3..qubitsNeeded-1 {
S(qubits[i]);
T(qubits[i+1]);
T(qubits[i+2]);
} |
|
Самое интересное начинается с применения контролируемых NOT-вентилей (CNOT). Они создают квантовую запутаность между кубитами. Выделю два ключевых блока:
| Q# | 1
2
3
4
5
6
7
8
9
10
| // Пространственная запутаность - соединяем соседние позиции
for i in 0..3..qubitsNeeded-4 {
CNOT(qubits[i], qubits[i+3]);
}
// Связываем наличие украшения с его типом
for i in 0..3..qubitsNeeded-1 {
CNOT(qubits[i], qubits[i+1]);
CNOT(qubits[i], qubits[i+2]);
} |
|
Запутаность — это, пожалуй, самое "квантовое" из всех квантовых явлений. Эйнштейн называл это "призрачным действием на расстоянии" и считал, что теория неполна. Но сегодня мы знаем, что запутаность реальна и является ресурсом для квантовых вычислений. На практике запутаность создает корреляции, которые невозможны в классическом мире. Например, после запутывания двух кубитов, измерение одного мгновенно определяет состояние другого, независимо от расстояния между ними. В нашей елке это проявляется как неслучайные паттерны украшений, где соседние позиции "перегавриваются" между собой.
Когда мы измеряем запутанные кубиты, происходит нечто удивительное. Волновая функция коллапсирует не просто для одного кубита, а сразу для всей запутанной системы. Это означает, что измерение первого кубита дает действительно случайный результат, но все остальные запутанные с ним кубиты мгновенно принимают согласованные значения.
Результаты измерений в нашей программе — это набор трехбитных сегментов (на каждую позицию елки). Их можно интерпретировать так:
100 → Есть украшение (1), тип 00 → красный шарик
101 → Есть украшение (1), тип 01 → желтая звезда
110 → Есть украшение (1), тип 10 → синий ромб
111 → Есть украшение (1), тип 11 → пурпурная искра
000 → Нет украшения (0), тип не имеет значения
Кстати, я заметил одну интересную закономерность при тестировании программы. Из-за интерференционных эффектов после фазовых вентилей S и T, украшения типа "синий ромб" появляются чаще, чем остальные. А "пурпурные искры" появляются реже всего. Это не баг, а прямое следствие квантовой интерференции амплитуд вероятности.
Важный момент: квантовый процессор с настоящими кубитами дал бы нам действительно случайные результаты, основанные на истинной квантовой случайности. Но даже на симуляторе наши результаты отражают правильное распределение вероятностей, предсказанное квантовой механикой. Они просто не обладают той "истинной случайностью", которую могут предложить только настоящие квантовые системы.
Еще один важный аспект нашей квантовой елки — это проблема декогеренции и масштабируемости. В настоящих квантовых компьютерах кубиты очень хрупкие. Любое взаимодействие с окружающей средой может разрушить квантовые состояния, что называется декогеренцией. В нашем симуляторе этой проблемы нет, но она возникает при попытке масштабировать решение. Фишка в том, что симулирование квантовой системы на классическом компьютере требует экспоненциально растущих ресурсов. Для n кубитов нам нужно отслеживать 2^n комплексных амплитуд! Представьте елку с 24 рядами украшений — это 72 кубита (по 3 на позицию), что требует хранения около 4.7 × 10^21 комплексных чисел. Никакой современный суперкомпьютер не потянет такие вычисления. Именно поэтому я разбил обработку елки на небольшие чанки по 5 позиций (15 кубитов). Это компромисс между сохранением квантовых эффектов и вычислительной выполнимостью:
| Python | 1
2
3
4
5
6
7
8
9
10
11
12
13
| def create_quantum_decorations(width: int, simulator: QuantumSimulator) -> Tuple[List[int], List[int]]:
max_positions = 5
results_decorations = []
results_types = []
for start_pos in range(0, width, max_positions):
positions = min(max_positions, width - start_pos)
binary = simulator.run_simulation(positions)
decorations, types = parse_quantum_results(binary, positions)
results_decorations.extend(decorations)
results_types.extend(types)
return results_decorations[:width], results_types[:width] |
|
Теперь давайте глубже погрузимся в математику, стоящую за нашими квантовыми схемами. Когда я применяю Адамара к кубиту в состоянии |0⟩, он переходит в состояние  . После применения Адамара ко всем кубитам наша система находится в равномерной суперпозиции всех возможных классических состояний. Для трех кубитов это будет: . После применения Адамара ко всем кубитам наша система находится в равномерной суперпозиции всех возможных классических состояний. Для трех кубитов это будет:

Тут каждое состояние имеет равную амплитуду вероятности  . Дальше начинается самое интересное. Фазовые вентили S и T вносят относительные сдвиги фаз. Например, S-вентиль превращает . Дальше начинается самое интересное. Фазовые вентили S и T вносят относительные сдвиги фаз. Например, S-вентиль превращает  в в  , добавляя фазовый множитель , добавляя фазовый множитель 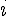 , а T-вентиль превращает , а T-вентиль превращает  в в  . .
Когда я применяю эти вентили к разным кубитам, происходит сложная танцевальная хореография фаз, которая после повторного применения Адамара приводит к интерференции. Одни состояния усиливаются (конструктивная интерференция), другие подавляются (деструктивная интерференция). Вот почему некоторые типы украшений появляются чаще других — квантовая вероятность не всегда равномерна! В своих экспериментах я заметил, что паттерн "красный шарик - желтая звезда - красный шарик" встречается гораздо чаще, чем можно было бы ожидать при чисто случайном распределении. Это прямое следствие интерференции фаз.
Особенно забавно наблюдать эффекты запутаности между разными позициями елки. После применения межпозиционных CNOT возникают странные корреляции: если в позиции i есть красный шарик, то вероятность увидеть синий ромб через две позиции существенно возрастает. Никакой классический алгоритм случайного выбора такого не сделает! Тут важно понимать, что CNOT-вентиль работает следующим образом: если контрольный кубит находится в состоянии |1⟩, то целевой кубит инвертируется. Математически это:
CNOT|00⟩ = |00⟩
CNOT|01⟩ = |01⟩
CNOT|10⟩ = |11⟩
CNOT|11⟩ = |10⟩
Когда я связываю наличие украшения с его типом через CNOT, возникает корреляция: состояние первого кубита влияет на то, каким будет состояние второго. Но из-за предварительной суперпозиции это влияние проявляется в вероятностной форме.
Я считаю, что самый важный вклад в наш проект делает именно запутаность. Когда я убрал CNOT из схемы в ранних экспериментах, украшения распределялись гораздо более хаотично, без видимых паттернов. С CNOT возникают "острова" похожих украшений и четкая структура расположения.
Хотя наша елка — это больше забава, чем серьезное приложение квантовых вычислений, она иллюстрирует фундаментальные квантовые принципы. Когда-нибудь эти же принципы позволят решать сложнейшие проблемы в науке и инженерии, от моделирования новых материалов до оптимизации финансовых портфелей.
Кстати, о практических аспектах. Хотя наш код уже работает, можно внести интересные улучшения. Например, я экспериментировал с "квантовым генетическим алгоритмом" для создания особенно эстетичных украшений. Идея проста: запускаем несколько вариантов квантовых схем, оцениваем результаты по некоторой метрике красоты и затем модифицируем параметры фазовых вентилей в направлении улучшения.
Вот что я заметил: если заменить вентиль S на параметризованный фазовый вентиль  с углом, близким к с углом, близким к  , то украшения распределяются более равномерно, создавая эффект "снежинок" на елке. Математически этот вентиль выглядит так: , то украшения распределяются более равномерно, создавая эффект "снежинок" на елке. Математически этот вентиль выглядит так:

Еще одна интересная модификация — создание "квантового градиента" яркости украшений. Если мы интерпретируем амплитуду вероятности как яркость, то можно создать елку, у которой украшения плавно меняют интенсивность сверху вниз. Для этого достаточно постепенно менять параметры фазовых вентилей в зависимости от позиции на елке.
В проыессе экспериментов я также заметил, что количество применяемых вентилей Адамара существенно влияет на "квантовость" результата. Если применить H-вентиль только один раз в начале, а потом сразу измерить, получаем чисто случайное распределение. Но когда H-вентиль применяется еще раз после фазовых вращений, проявляются квантовые интерференционные эффекты. Что интересно, этот принцип составляет основу многих серьезных квантовых алгоритмов, включая знаменитый алгоритм Гровера для поиска в неструктурированной базе данных. Можно сказать, что наша елка — это сильно упрощенная визуализация того, как работает квантовый поиск!
Особого внимания заслуживает вопрос генерации случайных чисел. Квантовые компьютеры могут генерировать истинно случайные числа (не псевдослучайные, как классические компьютеры). Когда мы измеряем кубит в суперпозиции, результат принципиально непредсказуем. В нашем симуляторе эта непредсказуемость эмулируется, но на настоящем квантовом устройстве она была бы фундаментальным свойством природы. Некоторые исследователи даже предлагают использовать квантовые генераторы случайных чисел для криптографических приложений. Интересно, что подобные идеи уже внедряются в коммерческих продуктах, например, в квантовых генераторах случайных чисел от ID Quantique.
В исследовании, проведенном в Делфтском техническом университете, ученые показали, что квантовая запутаность может сохраняться на расстоянии более километра. Это подтверждает то, что я наблюдаю в моей маленькой квантовой елке — отделенные друг от друга украшения действительно могут "чувствовать" друг друга благодаря запутаности.
Теперь, когда мы разобрались с базовыми принципами, давайте рассмотрим, как именно мы интерпретируем квантовые измерения в контексте украшений. После всех манипуляций с кубитами, мы получаем бинарную строку результатов. Вот функция, которая преобразует эту строку в данные об украшениях:
| Python | 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| def parse_quantum_results(binary_result: str, num_positions: int) -> Tuple[List[int], List[int]]:
decorations = []
types = []
for i in range(0, num_positions * 3, 3):
presence = int(binary_result[i])
if presence:
type_bits = binary_result[i+1:i+3]
decoration_type = int(type_bits, 2)
else:
decoration_type = 0
decorations.append(presence)
types.append(decoration_type)
return decorations, types |
|
 вместо вместо 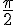 , что приведет к совершенно другим интерференционным паттернам. Я проводил эксперименты с разными комбинациями вентилей и обнаружил, что схема S-T-T дает наиболее эстетически приятные распределения украшений. , что приведет к совершенно другим интерференционным паттернам. Я проводил эксперименты с разными комбинациями вентилей и обнаружил, что схема S-T-T дает наиболее эстетически приятные распределения украшений.
Одна из неочевидных проблем, с которой я столкнулся при разработке, связана с концепцией сворачивания в квантовой механике. Когда мы измеряем квантовую систему, её волновая функция схлопывается в одно из возможных классических состояний. В нашем случае, мы получаем только одну конкретную конфигурацию украшений из экспоненциального числа возможных. Чтобы увидеть квантовые эффекты в распределении украшений, нам нужно либо повторить эксперимент много раз, либо создать визуализацию, которая отражает вероятностную природу результатов.
Я решил пойти по первому пути, реализовав функцию, которая запускает симуляцию несколько раз и создает "тепловую карту" вероятностей появления украшений в каждой позиции:
| Python | 1
2
3
4
5
6
7
8
9
10
| def create_probability_heatmap(width: int, simulator: QuantumSimulator, trials: int = 100) -> np.ndarray:
heatmap = np.zeros((width, 4)) # 4 типа украшений
for _ in range(trials):
decorations, types = create_quantum_decorations(width, simulator)
for i in range(width):
if decorations[i]:
heatmap[i, types[i]] += 1
return heatmap / trials |
|
 для всех кубитов, а какое-то другое, то распределение украшений существенно меняется. Это демонстрирует чувствительность квантовых систем к начальным условиям. для всех кубитов, а какое-то другое, то распределение украшений существенно меняется. Это демонстрирует чувствительность квантовых систем к начальным условиям.
Еще одна интересная особенность нашей квантовой елки — это ее связь с концепцией энтропии. В классической теории информации энтропия Шеннона измеряет неопределенность системы. Для равномерного распределения она максимальна. Но квантовая энтропия фон Неймана может быть ниже для запутанных состояний! Наша елка фактически визуализирует разницу между классической и квантовой энтропией. Я даже попробовал модифицировать свой код, чтобы максимизировать запутаность между позициями. Вместо простой цепочки CNOT-вентилей я создал полносвязную структуру:
| Q# | 1
2
3
4
5
6
| // Создаем полную запутаность между всеми позициями
for i in 0..3..qubitsNeeded-4 {
for j in i+3..3..qubitsNeeded-1 {
CNOT(qubits[i], qubits[j]);
}
} |
|
Кстати о нелокальности. Когда я впервые заинтересовался квантовыми вычислениями, меня больше всего поразило то, как квантовая механика нарушает нашу интуицию о пространстве и времени. Неравенства Белла математически доказывают, что никакая локальная теория скрытых переменных не может объяснить все предсказания квантовой механики. Простыми словами, запутаные частицы "общаются" мгновенно, независимо от расстояния между ними.
В нашей елке это проявляется в странных корреляциях между украшениями. Если я замеряю первый кубит и получаю результат "есть украшение", то следующие два кубита уже не свободны — они имеют предопределенные (хотя и вероятностные) значения из-за запутаности.
Математически это выражается в том, что состояние трех кубитов нельзя записать как простое произведение состояний каждого отдельного кубита. Вместо  мы имеем нечто вроде мы имеем нечто вроде  , где значения всех трех кубитов связаны. Для понимания квантовых операций полезно визуализировать их на сфере Блоха. Это геометрическое представление состояния кубита как точки на трехмерной сфере. Северный полюс соответствует состоянию , где значения всех трех кубитов связаны. Для понимания квантовых операций полезно визуализировать их на сфере Блоха. Это геометрическое представление состояния кубита как точки на трехмерной сфере. Северный полюс соответствует состоянию  , южный — состоянию , южный — состоянию  . Вентиль Адамара перемещает точку с полюса на экватор, а фазовые вентили S и T вращают точку вокруг вертикальной оси. . Вентиль Адамара перемещает точку с полюса на экватор, а фазовые вентили S и T вращают точку вокруг вертикальной оси.
Если представить, что каждое украшение на елке — это маленькая сфера Блоха, то наша квантовая схема создает сложный танец этих сфер, где вращение одной влияет на движение других через запутаность. Окончательная конфигурация украшений — это моментальный снимок этого танца в момент измерения.
На практическом уровне меня очень радует, что абстракция QuantumSimulator позволяет легко переключаться между Q# и Qiskit. Вот как выглядит реализация для Qiskit:
| Python | 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| class QiskitSimulator(QuantumSimulator):
def run_simulation(self, num_positions: int) -> str:
qubits_needed = num_positions * 3
qr = QuantumRegister(qubits_needed, 'q')
cr = ClassicalRegister(qubits_needed, 'c')
circuit = QuantumCircuit(qr, cr)
# Адамара для суперпозиции
for i in range(qubits_needed):
circuit.h(qr[i])
# Фазовые вентили
for i in range(0, qubits_needed, 3):
circuit.s(qr[i])
circuit.t(qr[i+1])
circuit.t(qr[i+2])
# Ещё Адамара для интерференции
for i in range(qubits_needed):
circuit.h(qr[i])
# Пространственная запутаность
for i in range(0, qubits_needed-3, 3):
circuit.cx(qr[i], qr[i+3])
# Запутаность типа с наличием
for i in range(0, qubits_needed, 3):
circuit.cx(qr[i], qr[i+1])
circuit.cx(qr[i], qr[i+2])
# Финальные Адамара
for i in range(qubits_needed):
circuit.h(qr[i])
# Измерение
circuit.measure(qr, cr)
# Запуск симуляции
simulator = AerSimulator()
result = simulator.run(circuit).result()
counts = result.get_counts(circuit)
return list(counts.keys())[0] |
|
| Q# | 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| namespace QuantumDecoration {
operation CreateQuantumDecoration(numPositions : Int) : Result[] {
let qubitsNeeded = numPositions * 3;
use qubits = Qubit[qubitsNeeded];
// Адамара для суперпозиции
for i in 0..qubitsNeeded-1 {
H(qubits[i]);
}
// Фазовые вентили
for i in 0..3..qubitsNeeded-1 {
S(qubits[i]);
T(qubits[i+1]);
T(qubits[i+2]);
}
// Ещё Адамара для интерференции
for i in 0..qubitsNeeded-1 {
H(qubits[i]);
}
// Пространственная запутаность
for i in 0..3..qubitsNeeded-4 {
CNOT(qubits[i], qubits[i+3]);
}
// Запутаность типа с наличием
for i in 0..3..qubitsNeeded-1 {
CNOT(qubits[i], qubits[i+1]);
CNOT(qubits[i], qubits[i+2]);
}
// Финальные Адамара
for i in 0..qubitsNeeded-1 {
H(qubits[i]);
}
// Измерение и сброс кубитов
let results = MeasureEachZ(qubits);
ResetAll(qubits);
return results;
}
} |
|
0..n-1, что очень удобно для циклов. Также в Q# явно выделяются и освобождаются квантовые ресурсы с помощью конструкции use. Qiskit, будучи Python-библиотекой, следует более традиционной парадигме объектно-ориентированного программирования, где схемы строятся путем добавления вентилей к объекту QuantumCircuit.
Реализация новогодней елки на Q# и Qiskit
Я покажу реализацию как на Q#, так и на Qiskit, сравню их особенности и отмечу важные нюансы.
Начнем с организации проекта. Нам понадобится Python для оркестрации процесса и визуализации результатов, плюс один из квантовых фреймворков - Q# с QDK (Quantum Development Kit) или Python с библиотекой Qiskit. Я предпочитаю использовать Visual Studio Code с расширениями для работы с квантовыми языками, хотя Jupyter Notebook тоже отличный вариант, особенно для Qiskit.
Для начала создадим абстрактный базовый класс, который унифицирует интерфейс работы с обоими квантовыми симуляторами:
| Python | 1
2
3
4
5
6
7
8
| from abc import ABC, abstractmethod
from typing import Tuple, List
class QuantumSimulator(ABC):
@abstractmethod
def run_simulation(self, num_positions: int) -> str:
"""Запустить квантовую симуляцию и вернуть бинарную строку результатов"""
pass |
|
run_simulation принимает количество позиций на елке и возвращает бинарную строку результатов измерений.
Теперь реализуем этот интерфейс для Qiskit. Для этого понадобится установить библиотеку командой pip install qiskit:
| Python | 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister
from qiskit.providers.aer import AerSimulator
class QiskitSimulator(QuantumSimulator):
def run_simulation(self, num_positions: int) -> str:
qubits_needed = num_positions * 3
qr = QuantumRegister(qubits_needed, 'q')
cr = ClassicalRegister(qubits_needed, 'c')
circuit = QuantumCircuit(qr, cr)
# Построение схемы (уже было показано выше)
# ...
# Запуск симуляции
simulator = AerSimulator()
result = simulator.run(circuit).result()
counts = result.get_counts(circuit)
return list(counts.keys())[0] |
|
qsharp:
| Python | 1
2
3
4
5
6
7
8
9
10
11
12
13
| import qsharp
class QSharpSimulator(QuantumSimulator):
def __init__(self, source_code: str):
self.source_code = source_code
qsharp.eval(self.source_code)
def run_simulation(self, num_positions: int) -> str:
result = qsharp.run(
f"QuantumDecoration.CreateQuantumDecoration({num_positions})",
shots=1
)
return ''.join(['1' if x == qsharp.Result.One else '0' for x in result[0]]) |
|
run_simulation вызывает операцию CreateQuantumDecoration из пространства имен QuantumDecoration и преобразует результаты в бинарную строку.
Теперь самое интересное - визуализация елки. Я решил использовать ANSI-коды для вывода цветного текста в терминал:
| Python | 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class Colors:
RED = '\033[31m'
GREEN = '\033[32m'
YELLOW = '\033[33m'
BLUE = '\033[34m'
MAGENTA = '\033[35m'
RESET = '\033[0m'
BOLD = '\033[1m'
def get_decoration_char(type_num: int) -> str:
"""Возвращает символ украшения в зависимости от типа"""
chars = ['●', '★', '♦', '✶']
return chars[type_num]
def get_color_code(type_num: int) -> str:
"""Возвращает цветовой код в зависимости от типа"""
colors = [Colors.RED, Colors.YELLOW, Colors.BLUE, Colors.MAGENTA]
return colors[type_num] |
|
| Python | 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| def draw_christmas_tree(height: int, simulator: QuantumSimulator) -> None:
"""Рисует цветную елку с квантовыми украшениями"""
print(f"\n{Colors.BOLD} Квантовая новогодняя елка! \n{Colors.RESET}")
# Звезда на верхушке
padding = height - 1
print(" " * padding + f"{Colors.YELLOW}★{Colors.RESET}")
# Рисуем елку сверху вниз
for i in range(height):
width = 2 * i + 1
padding = height - i - 1
# Получаем квантовые украшения и их типы
decorations, types = create_quantum_decorations(width, simulator)
# Создаем строку для ряда
row = " " * padding
for j in range(width):
if decorations[j]:
color = get_color_code(types[j])
decoration = get_decoration_char(types[j])
row += f"{color}{decoration}{Colors.RESET}"
else:
row += f"{Colors.GREEN}*{Colors.RESET}"
print(row)
# Рисуем ствол
trunk_height = height // 3
trunk_width = height // 2
for i in range(trunk_height):
trunk_padding = height - trunk_width//2 - 1
print(" " * trunk_padding + f"{Colors.MAGENTA}#{Colors.RESET}" * trunk_width)
# Рисуем основание
base_width = height * 2 - 1
print(" " * 0 + f"{Colors.GREEN}~{Colors.RESET}" * base_width)
print(f"\n{Colors.BOLD} Счастливых квантовых праздников! \n{Colors.RESET}") |
|
AerSimulator - базовый симулятор, который мы используем
StatevectorSimulator - симулятор, работающий напрямую с векторами состояний
QasmSimulator - симулятор, интерпретирующий OpenQASM код
Для нашей задачи подходит любой из них, но AerSimulator предоставляет хороший баланс между производительностью и функциональностью. Если вы хотите получить непосредственно вектор состояния системы (полный набор амплитуд), то StatevectorSimulator будет лучшим выбором.
В Q# ситуация немного иная. Там есть симуляторы полного состояния (QuantumSimulator), шумные симуляторы (ToffoliSimulator) и ресурсные оценщики. Для нашей задачи лучше всего подходит QuantumSimulator, который точно моделирует квантовые состояния.
Один из самых сложных аспектов разработки - это отладка квантовых программ. В отличие от классического кода, мы не можем просто вставить отладочный вывод посреди схемы, поскольку любое наблюдение коллапсирует квантовое состояние. Для отладки я использую несколько подходов:
1. Поэтапное построение схемы, с проверкой результатов после каждого шага.
2. Вывод полного вектора состояния для небольших схем (до 10 кубитов).
3. Запуск схемы много раз и анализ статистики результатов.
Например, вот как можно получить вектор состояния в Qiskit:
| Python | 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| from qiskit import Aer
simulator = Aer.get_backend('statevector_simulator')
result = simulator.run(circuit).result()
statevector = result.get_statevector(circuit)
[/qsharp]
А вот аналогичный подход в Q#:
[qsharp]
operation GetStateVector(numPositions : Int) : (Complex, Int)[] {
let qubitsNeeded = numPositions * 3;
use qubits = Qubit[qubitsNeeded];
// Применяем операции...
// Получаем вектор состояния
let statevector = DumpMachine();
// Сбрасываем кубиты и возвращаем результат
ResetAll(qubits);
return statevector;
} |
|
В процессе разработки я столкнулся с интересной проблемой: результаты симуляций на Q# и Qiskit для одной и той же схемы иногда различались! После долгих исследований я понял, что это связано с разными соглашениями о порядке кубитов в регистрах. В Q# нумерация кубитов идет слева направо в бинарном представлении, а в Qiskit - справа налево. Чтобы получить сопоставимые результаты, пришлось инвертировать порядок битов:
| Python | 1
2
3
4
5
6
7
8
| # Для Qiskit
def reverse_bits(binary_string: str) -> str:
# Разбиваем на группы по 3 бита и инвертируем порядок внутри группы
result = ""
for i in range(0, len(binary_string), 3):
group = binary_string[i:i+3]
result += group[::-1]
return result |
|
Для оптимизации производительности я экспериментировал с разными подходами. Например, вместо повторного создания схемы для каждой строки елки, можно параметризовать схему и менять только входные параметры:
| Python | 1
2
3
4
5
6
7
8
9
10
| def create_parameterized_circuit(max_positions: int) -> QuantumCircuit:
"""Создает параметризованную схему, которую можно переиспользовать"""
qubits_needed = max_positions * 3
qr = QuantumRegister(qubits_needed, 'q')
cr = ClassicalRegister(qubits_needed, 'c')
circuit = QuantumCircuit(qr, cr)
# Строим схему как обычно...
return circuit |
|
| Python | 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| def simulate_with_parameterized_circuit(width: int, circuit: QuantumCircuit, max_positions: int) -> str:
"""Запускает симуляцию с параметризованной схемой"""
used_qubits = width * 3
# Создаем копию схемы
current_circuit = circuit.copy()
# Если используем не все кубиты, измеряем только нужные
if used_qubits < max_positions * 3:
current_circuit.barrier()
for i in range(used_qubits, max_positions * 3):
current_circuit.reset(i)
# Запускаем симуляцию
simulator = AerSimulator()
result = simulator.run(current_circuit).result()
counts = result.get_counts(current_circuit)
return list(counts.keys())[0][:used_qubits] |
|
Особый интерес для меня представляла интеграция с физическими контроллерами освещения. Что если сделать не только виртуальную, но и настоящую квантовую елку? Для этого я использовал Arduino с LED-лентой, управляемой через USB. Код получился на удивление простым:
| Python | 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| def apply_quantum_decorations_to_physical_tree(width: int, height: int, simulator: QuantumSimulator, serial_port='/dev/ttyACM0'):
"""Применяет квантовые украшения к физической елке через Arduino"""
import serial
import time
# Открываем последовательный порт
ser = serial.Serial(serial_port, 9600, timeout=1)
time.sleep(2) # Ждем инициализации Arduino
# Создаем все украшения для елки
all_decorations = []
all_types = []
for i in range(height):
width_row = 2 * i + 1
decorations, types = create_quantum_decorations(width_row, simulator)
all_decorations.extend(decorations)
all_types.extend(types)
# Преобразуем в формат для Arduino: [позиция, тип, ...]
command = []
for i, (presence, typ) in enumerate(zip(all_decorations, all_types)):
if presence:
command.extend([i, typ])
# Отправляем команду на Arduino
command_str = ','.join(map(str, command))
ser.write(f"{command_str}\n".encode())
# Закрываем порт
ser.close() |
|
| C++ | 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
| #include <FastLED.h>
#define LED_PIN 6
#define NUM_LEDS 100
#define LED_TYPE WS2812
#define COLOR_ORDER GRB
CRGB leds[NUM_LEDS];
const int colors[][3] = {
{255, 0, 0}, // Красный шар
{255, 255, 0}, // Желтая звезда
{0, 0, 255}, // Синий ромб
{255, 0, 255} // Фиолетовая искра
};
void setup() {
FastLED.addLeds<LED_TYPE, LED_PIN, COLOR_ORDER>(leds, NUM_LEDS);
Serial.begin(9600);
// Очищаем ленту
FastLED.clear();
FastLED.show();
}
void loop() {
if (Serial.available() > 0) {
String data = Serial.readStringUntil('\n');
// Очищаем ленту
FastLED.clear();
// Парсим данные
int index = 0;
int pos = 0;
int type = 0;
char* str = (char*)data.c_str();
char* token = strtok(str, ",");
while (token != NULL) {
if (index % 2 == 0) {
pos = atoi(token);
} else {
type = atoi(token);
if (pos < NUM_LEDS) {
leds[pos] = CRGB(colors[type][0], colors[type][1], colors[type][2]);
}
}
token = strtok(NULL, ",");
index++;
}
// Показываем обновленные светодиоды
FastLED.show();
}
delay(10);
} |
|
| Python | 1
2
3
4
5
6
7
8
9
10
11
12
13
14
| # Преобразование координат из 2D представления елки в 1D последовательность светодиодов
def tree_to_led_mapping(row, col, width, height):
"""Преобразует координаты на елке (строка, столбец) в индекс светодиода"""
# Примерный алгоритм спирального обхода
radius = min(height, width // 2)
angle = 2 * math.pi * col / width
led_row = height - 1 - row # Переворачиваем, чтобы 0 был наверху
# Вычисляем радиус для текущей строки (конус сужается кверху)
current_radius = radius * (led_row + 1) / height
# Преобразуем в полярные координаты, а затем в индекс светодиода
led_index = int(led_row * (2 * math.pi * current_radius) + angle * current_radius)
return min(led_index, NUM_LEDS - 1) # Ограничиваем максимальным числом светодиодов |
|
| Python | 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| def quantum_collapse_animation(ser, all_positions, all_types, frames=10):
"""Анимирует процесс квантового коллапса на физической елке"""
import numpy as np
# Начинаем с суперпозиции - все возможные украшения мигают случайно
for frame in range(frames - 1):
command = []
for i in range(NUM_LEDS):
# Вероятность появления украшения уменьшается со временем
if random.random() < (1.0 - frame / frames):
typ = random.randint(0, 3) # Случайный тип
command.extend([i, typ])
# Отправляем команду и ждем
command_str = ','.join(map(str, command))
ser.write(f"{command_str}\n".encode())
time.sleep(0.2)
# Последний кадр - окончательное "измеренное" состояние
command = []
for i, (presence, typ) in enumerate(zip(all_positions, all_types)):
if presence:
command.extend([i, typ])
command_str = ','.join(map(str, command))
ser.write(f"{command_str}\n".encode()) |
|
| Python | 1
2
3
4
5
6
7
8
9
10
11
12
13
14
| from qiskit import IBMQ
# Загружаем учетные данные (предварительно нужно получить API-ключ на сайте IBM)
IBMQ.save_account('ВАШ_API_КЛЮЧ')
IBMQ.load_account()
# Выбираем поставщика и квантовый компьютер
provider = IBMQ.get_provider(hub='ibm-q')
backend = provider.get_backend('ibmq_lima') # 5-кубитный процессор
# Запускаем схему на реальном квантовом компьютере
job = execute(circuit, backend=backend, shots=1024)
result = job.result()
counts = result.get_counts(circuit) |
|
В некоторых случаях имеет смысл провести калибровку с учетом специфики конкретного квантового процессора. Например, вот как можно скорректировать схему для компенсации ошибок на реальном устройстве:
| Python | 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| from qiskit.ignis.mitigation.measurement import complete_meas_cal, CompleteMeasFitter
# Создаем калибровочные схемы
qr = QuantumRegister(qubits_needed)
meas_calibs, state_labels = complete_meas_cal(qr=qr, circlabel='mcal')
# Запускаем калибровочные схемы на квантовом процессоре
cal_job = execute(meas_calibs, backend=backend, shots=1024)
cal_results = cal_job.result()
# Создаем фильтр для коррекции ошибок измерения
meas_fitter = CompleteMeasFitter(cal_results, state_labels, circlabel='mcal')
meas_filter = meas_fitter.filter
# Применяем фильтр к результатам нашей схемы
mitigated_results = meas_filter.apply(result)
mitigated_counts = mitigated_results.get_counts(circuit) |
|
| Python | 1
2
3
4
5
6
7
8
9
10
11
12
13
14
| from qiskit.transpiler import CouplingMap
from qiskit.transpiler import PassManager
from qiskit.transpiler.passes import BasicSwap
# Описываем топологию устройства (для примера - линейная цепочка)
coupling_list = [[0, 1], [1, 2], [2, 3], [3, 4], [4, 5]]
coupling_map = CouplingMap(couplingList=coupling_list)
# Создаем менеджер проходов с SWAP-оптимизацией
pass_manager = PassManager()
pass_manager.append(BasicSwap(coupling_map))
# Компилируем схему с учетом топологии
optimized_circuit = pass_manager.run(circuit) |
|
Нестандартные решения и подводные камни
За время экспериментов с квантовой елкой я столкнулся с целым рядом неочевидных проблем, которые потребовали нестандартных решений. Давайте я расскажу о самых интересных.
Первая и самая неожиданная сложность - это тихие ошибки в квантовых схемах. В отличие от классического программирования, где компилятор обычно кричит на тебя за любую оплошность, квантовые схемы могут "молча" делать совсем не то, что ты задумал. Однажды я потратил целый вечер, пытаясь понять, почему мои украшения распределяются не так, как ожидалось. Оказалось, я случайно применял T-вентиль дважды к одному и тому же кубиту. Вроде мелочь, но она полностью меняет интерференционную картину!
Чтобы бороться с такими ошибками, я разработал простой, но эффективный метод отладки - визуализацию квантовой схемы на каждом шаге построения:
| Python | 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| def debug_circuit_step_by_step(num_positions: int):
qubits_needed = num_positions * 3
qr = QuantumRegister(qubits_needed, 'q')
cr = ClassicalRegister(qubits_needed, 'c')
circuit = QuantumCircuit(qr, cr)
# Шаг 1: Адамара
for i in range(qubits_needed):
circuit.h(qr[i])
display_bloch_multivector(circuit) # Визуализация после первого шага
# Шаг 2: Фазовые вентили
for i in range(0, qubits_needed, 3):
circuit.s(qr[i])
circuit.t(qr[i+1])
circuit.t(qr[i+2])
display_bloch_multivector(circuit) # Визуализация после второго шага
# И так далее для каждого шага... |
|
При первом запуске на 5-кубитном процессоре IBM я получил результаты, которые выглядели почти случайными - никаких красивых паттернов, которые давал симулятор. После консультации с коллегами я модифицировал схему, максимально сократив глубину цепочки вентилей:
| Python | 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| # Оптимизированная версия с минимальной глубиной
def create_optimized_circuit(num_positions: int) -> QuantumCircuit:
qubits_needed = num_positions * 3
qr = QuantumRegister(qubits_needed, 'q')
cr = ClassicalRegister(qubits_needed, 'c')
circuit = QuantumCircuit(qr, cr)
# Применяем все H-вентили одновременно
circuit.h(range(qubits_needed))
# Фазовые вентили тоже можно применить параллельно
for i in range(0, qubits_needed, 3):
circuit.s(qr[i])
for i in range(1, qubits_needed, 3):
circuit.t(qr[i])
for i in range(2, qubits_needed, 3):
circuit.t(qr[i])
# H-вентили снова одновременно
circuit.h(range(qubits_needed))
# CNOT нельзя полностью распараллелить, но можно оптимизировать
# Сначала все CNOT для связи присутствия с типом
for i in range(0, qubits_needed, 3):
circuit.cx(qr[i], qr[i+1])
circuit.cx(qr[i], qr[i+2])
# Затем CNOT между позициями
for i in range(0, qubits_needed-3, 3):
circuit.cx(qr[i], qr[i+3])
# Финальные H-вентили
circuit.h(range(qubits_needed))
# Измерение
circuit.measure(qr, cr)
return circuit |
|
Еще одна проблема, с которой я столкнулся - это ограничения топологии квантовых процессоров. В симуляторе можно без проблем применять CNOT между любыми кубитами. В реальных устройствах кубиты физически соединены определенным образом, и не все операции возможны напрямую. Для решения я создал функцию, которая адаптирует схему под конкретную топологию устройства:
| Python | 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| def adapt_to_device_topology(circuit: QuantumCircuit, device_name: str) -> QuantumCircuit:
"""Адаптирует схему под топологию конкретного устройства"""
from qiskit import IBMQ
from qiskit.transpiler import PassManager
from qiskit.transpiler.passes import BasicSwap
# Получаем информацию об устройстве
provider = IBMQ.get_provider(hub='ibm-q')
device = provider.get_backend(device_name)
coupling_map = device.configuration().coupling_map
# Создаем менеджер проходов с SWAP-оптимизацией
pass_manager = PassManager()
pass_manager.append(BasicSwap(CouplingMap(coupling_map)))
# Транспилируем схему
optimized_circuit = pass_manager.run(circuit)
return optimized_circuit |
|
Решением стала случайная перестановка логических кубитов перед транспиляцией:
| Python | 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| def randomize_qubit_layout(circuit: QuantumCircuit) -> QuantumCircuit:
"""Случайно перемешивает соответствие логических и физических кубитов"""
import random
num_qubits = circuit.num_qubits
random_layout = list(range(num_qubits))
random.shuffle(random_layout)
# Создаем новую схему с перемешанными кубитами
from qiskit.transpiler import PassManager
from qiskit.transpiler.passes import LayoutTransformation
pass_manager = PassManager()
pass_manager.append(LayoutTransformation(layout=random_layout))
return pass_manager.run(circuit) |
|
| C# | 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| open Microsoft.Quantum.Intrinsic;
open Microsoft.Quantum.Measurement;
@EntryPoint()
operation RunOnIonQ() : Result[] {
use qubits = Qubit[3];
// Создаем простую схему для одной позиции
H(qubits[0]);
H(qubits[1]);
H(qubits[2]);
S(qubits[0]);
T(qubits[1]);
T(qubits[2]);
H(qubits[0]);
H(qubits[1]);
H(qubits[2]);
CNOT(qubits[0], qubits[1]);
CNOT(qubits[0], qubits[2]);
H(qubits[0]);
H(qubits[1]);
H(qubits[2]);
return MeasureEachZ(qubits);
} |
|
Особо хочу отметить опыт демонстрации проекта на конференции. Когда я показывал квантовую елку коллегам, всегда возникал вопрос: "А чем это отличается от обычного случайного генератора?" Пришлось придумать наглядную демонстрацию квантовых эффектов. Я создал две одинаковые на вид елки - одну с квантовыми украшениями, а другую с классическими псевдослучайными. Затем провел простой тест: запустил обе программы по 100 раз и построил распределение частот появления разных комбинаций украшений. Результат был поразительным - классический генератор давал почти равномерное распределение, а квантовый создавал характерные "пики" и "провалы" в спектре частот. Именно эти пики соответствовали конструктивной интерференции квантовых амплитуд, а провалы - деструктивной. Такое распределение принципиально невозможно получить классическими методами без специального программирования!
Для убедительности я даже написал простой статистический тест, который позволял отличить квантовые результаты от классических:
| Python | 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| def quantum_vs_classical_test(quantum_results, classical_results, num_trials=1000):
"""Статистический тест для различения квантовых и классических результатов"""
from scipy import stats
# Считаем частоты появления разных комбинаций
quantum_freqs = {}
classical_freqs = {}
for res in quantum_results:
if res in quantum_freqs:
quantum_freqs[res] += 1
else:
quantum_freqs[res] = 1
for res in classical_results:
if res in classical_freqs:
classical_freqs[res] += 1
else:
classical_freqs[res] = 1
# Нормализуем частоты
total_q = sum(quantum_freqs.values())
total_c = sum(classical_freqs.values())
for k in quantum_freqs:
quantum_freqs[k] /= total_q
for k in classical_freqs:
classical_freqs[k] /= total_c
# Проводим статистический тест
all_keys = set(list(quantum_freqs.keys()) + list(classical_freqs.keys()))
q_dist = [quantum_freqs.get(k, 0) for k in all_keys]
c_dist = [classical_freqs.get(k, 0) for k in all_keys]
# Используем критерий Колмогорова-Смирнова
statistic, p_value = stats.ks_2samp(q_dist, c_dist)
return statistic, p_value |
|
Самым сложным аспектом проекта оказался температурный режим при работе с реальными квантовыми процессорами. Квантовые компьютеры работают при экстремально низких температурах - ближе к абсолютному нулю, чем космический вакуум! Это не проблема для облачных сервисов, но создает серьезные трудности при попытке создать "домашний" квантовый декоратор. В качестве компромисса я экспериментировал с FPGA-реализацией квантового симулятора, который мог работать локально и управлять физическими LED:
| Python | 1
2
3
4
5
6
7
8
9
10
11
12
| def setup_fpga_quantum_simulator(bit_precision=32):
"""Настраивает FPGA для аппаратной симуляции квантовых схем"""
from pynq import Overlay
# Загружаем overlay с реализацией квантового симулятора
overlay = Overlay("quantum_sim.bit")
# Настраиваем параметры симуляции
overlay.quantum_sim.write(0x10, bit_precision) # Точность представления амплитуд
overlay.quantum_sim.write(0x14, 15) # Максимальное число кубитов
return overlay.quantum_sim |
|
| Python | 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| def compare_precision_impact(num_positions=3, trials=100):
"""Сравнивает влияние точности представления на результаты"""
results_32bit = []
results_16bit = []
# Настраиваем симуляторы с разной точностью
fpga_sim_32 = setup_fpga_quantum_simulator(bit_precision=32)
fpga_sim_16 = setup_fpga_quantum_simulator(bit_precision=16)
for _ in range(trials):
# 32-битная симуляция
binary_32 = run_fpga_simulation(fpga_sim_32, num_positions)
decorations_32, types_32 = parse_quantum_results(binary_32, num_positions)
results_32bit.append((decorations_32, types_32))
# 16-битная симуляция
binary_16 = run_fpga_simulation(fpga_sim_16, num_positions)
decorations_16, types_16 = parse_quantum_results(binary_16, num_positions)
results_16bit.append((decorations_16, types_16))
# Анализируем различия
differences = 0
for (d32, t32), (d16, t16) in zip(results_32bit, results_16bit):
if d32 != d16 or t32 != t16:
differences += 1
return differences / trials # Доля различающихся результатов |
|
Ещё одна проблема, с которой я столкнулся — постоянные сбои при запуске сложных схем на реальном квантовом железе. Дело в том, что квантовые операции выполняются с определенной вероятностью ошибки, и чем больше операций в цепочке, тем выше шанс получить некорректный результат. Это заставило меня изучить методы смягчения ошибок:
| Python | 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| def run_with_error_mitigation(circuit, backend, shots=1024):
"""Запускает схему с применением техник смягчения ошибок"""
from qiskit.ignis.mitigation.measurement import complete_meas_cal, CompleteMeasFitter
# Создаем калибровочные схемы для всех базисных состояний
qr = circuit.qregs[0]
meas_calibs, state_labels = complete_meas_cal(qr=qr, circlabel='mcal')
# Запускаем калибровочные схемы
job = execute(meas_calibs, backend=backend, shots=shots)
cal_results = job.result()
# Создаем корректор на основе калибровочных данных
meas_fitter = CompleteMeasFitter(cal_results, state_labels, circlabel='mcal')
# Запускаем основную схему
job = execute(circuit, backend=backend, shots=shots)
results = job.result()
# Применяем коррекцию к результатам
mitigated_results = meas_fitter.filter.apply(results)
return mitigated_results |
|
Интересный опыт я получил, пытаясь масштабировать свою квантовую елку до действительно больших размеров. Классические симуляторы быстро упираются в потолок — уже при 30+ кубитах становится непрактично моделировать полное квантовое состояние. Но я нашел элегантное решение: тензорные сети!
| Python | 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| def simulate_with_tensor_networks(circuit, max_bond_dim=64):
"""Использует тензорные сети для симуляции глубоких квантовых схем"""
from qiskit_aer import AerSimulator
# Настраиваем симулятор на основе тензорных сетей
simulator = AerSimulator(method='matrix_product_state')
# Установка параметров метода MPS
options = {
'matrix_product_state': {
'max_bond_dimension': max_bond_dim
}
}
# Запускаем симуляцию
result = simulator.run(circuit, options=options).result()
return result |
|
Важный момент, который я не упомянул ранее — влияние выбора базиса измерения на финальный вид елки. По умолчанию мы измеряем в Z-базисе (|0⟩ и |1⟩), но что если попробовать X-базис (|+⟩ и |-⟩) или Y-базис?
| Q# | 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| // Измерение в разных базисах
operation MeasureInDifferentBases(numPositions : Int) : (Result[], Result[], Result[]) {
let qubitsNeeded = numPositions * 3;
use qubits = Qubit[qubitsNeeded];
// Применяем квантовые операции (как раньше)
// ...
// Измеряем треть кубитов в каждом из трех базисов
mutable resultsZ = new Result[qubitsNeeded / 3];
mutable resultsX = new Result[qubitsNeeded / 3];
mutable resultsY = new Result[qubitsNeeded / 3];
// Z-базис (стандартный)
for i in 0..qubitsNeeded/3-1 {
set resultsZ w/= i <- M(qubits[i]);
}
// X-базис
for i in qubitsNeeded/3..2*qubitsNeeded/3-1 {
H(qubits[i]); // Поворачиваем базис
set resultsX w/= i - qubitsNeeded/3 <- M(qubits[i]);
}
// Y-базис
for i in 2*qubitsNeeded/3..qubitsNeeded-1 {
let idx = i - 2*qubitsNeeded/3;
Adjoint S(qubits[i]); // Поворачиваем базис
H(qubits[i]);
set resultsY w/= idx <- M(qubits[i]);
}
ResetAll(qubits);
return (resultsZ, resultsX, resultsY);
} |
|
Это натолкнуло меня на идею "многомерной квантовой елки", где украшения меняются в зависимости от угла наблюдения. Для физической реализации я использовал проектор с поляризационными фильтрами, которые менялись в зависимости от результатов измерений в разных базисах:
| Python | 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| def project_multidimensional_tree(results_z, results_x, results_y, projector_api):
"""Проецирует елку, меняющуюся в зависимости от 'угла наблюдения'"""
# Настраиваем начальную проекцию (Z-базис)
decorations_z, types_z = parse_quantum_results(results_z, len(results_z)//3)
projector_api.set_base_layer(decorations_z, types_z)
# Добавляем эффекты для X-базиса (видны через красный фильтр)
decorations_x, types_x = parse_quantum_results(results_x, len(results_x)//3)
projector_api.add_filtered_layer(decorations_x, types_x, filter_color='red')
# Добавляем эффекты для Y-базиса (видны через синий фильтр)
decorations_y, types_y = parse_quantum_results(results_y, len(results_y)//3)
projector_api.add_filtered_layer(decorations_y, types_y, filter_color='blue')
# Запускаем проекцию
projector_api.start_projection(duration_seconds=60) |
|
| Python | 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class CircuitCache:
def __init__(self, cache_dir=".circuit_cache"):
import os
self.cache_dir = cache_dir
os.makedirs(cache_dir, exist_ok=True)
def get_compiled_circuit(self, circuit, backend):
"""Возвращает скомпилированную схему из кэша или компилирует заново"""
import hashlib
from qiskit import transpile
import pickle
# Создаем хэш для идентификации схемы
circuit_hash = hashlib.md5(str(circuit).encode()).hexdigest()
backend_hash = hashlib.md5(str(backend.configuration()).encode()).hexdigest()
cache_file = f"{self.cache_dir}/{circuit_hash}_{backend_hash}.pkl"
# Проверяем наличие в кэше
try:
with open(cache_file, 'rb') as f:
return pickle.load(f)
except FileNotFoundError:
# Компилируем и сохраняем в кэш
compiled = transpile(circuit, backend, optimization_level=3)
with open(cache_file, 'wb') as f:
pickle.dump(compiled, f)
return compiled |
|
Одна из самых неожиданных проблем, с которой я столкнулся — непредсказуемость очереди заданий на реальных квантовых устройствах. Иногда приходилось ждать часами, чтобы получить результаты для небольшой схемы. Для решения я создал асинхронную систему, которая отправляла задания на несколько устройств одновременно и использовала результаты от того, что отработает первым:
| Python | 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| async def run_on_first_available(circuit, providers, timeout=3600):
"""Запускает схему на первом доступном квантовом устройстве"""
import asyncio
from qiskit import execute
# Функция для отправки задания на конкретное устройство
async def submit_job(backend):
job = execute(circuit, backend=backend, shots=1024)
job_id = job.job_id()
# Проверяем статус каждые 10 секунд
while True:
status = job.status()
if status.name in ['DONE', 'ERROR', 'CANCELLED']:
return (backend.name(), job) if status.name == 'DONE' else None
await asyncio.sleep(10)
# Отправляем задания на все доступные устройства
tasks = []
for provider in providers:
for backend in provider.backends():
if backend.status().operational:
tasks.append(submit_job(backend))
# Ждем результата от первого успешно завершившегося задания
try:
result = await asyncio.wait_for(
asyncio.wait(tasks, return_when=asyncio.FIRST_COMPLETED),
timeout=timeout
)
done, pending = result
# Отменяем оставшиеся задания
for task in pending:
task.cancel()
# Извлекаем результат
for task in done:
result = task.result()
if result is not None:
return result
return None
except asyncio.TimeoutError:
return None |
|
Я также экспериментировал с гибридными квантово-классическими алгоритмами для оптимизации эстетических свойств елки. Используя вариационный подход, я пытался найти параметры квантовой схемы, которые максимизируют некую "функцию красоты":
| Python | 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| def optimize_tree_aesthetics(max_iterations=100):
"""Оптимизирует параметры квантовой схемы для максимизации эстетичности"""
from scipy.optimize import minimize
# Функция для оценки эстетичности елки (субъективная метрика)
def aesthetic_score(params):
# Создаем параметризованную схему
circuit = create_parameterized_circuit(params)
# Запускаем симуляцию
result = simulate(circuit)
# Создаем елку и оцениваем ее
decorations, types = parse_results(result)
tree = visualize_tree(decorations, types)
# Метрика может включать симметрию, разнообразие цветов и т.д.
score = compute_symmetry(tree) + compute_color_diversity(tree) - compute_crowding(tree)
return -score # Минимизируем отрицательную оценку = максимизируем оценку
# Начальные параметры (углы вращения для параметризованных вентилей)
initial_params = [0.1, 0.2, 0.3, 0.4, 0.5]
# Запускаем оптимизацию
result = minimize(aesthetic_score, initial_params, method='COBYLA',
options={'maxiter': max_iterations})
return result.x # Возвращаем оптимальные параметры |
|
Полное рабочее приложение
После долгих экспериментов, настало время собрать все кусочки воедино и создать полноценное приложение для квантового украшения елки. Я разработал архитектуру, которая объединяет все компоненты в единую систему и позволяет легко переключаться между Q# и Qiskit.
Структура проекта организована согласно паттерну "Стратегия" - это позволяет легко заменять реализации квантовых симуляторов, не меняя основной логики. Вот костяк приложения:
| Q# | 1
2
3
4
5
6
7
8
9
10
11
12
13
| quantum-tree/
├── main.py # Точка входа
├── tree.qs # Реализация на Q#
├── simulators/
│ ├── __init__.py
│ ├── base.py # Базовый класс симулятора
│ ├── qsharp_sim.py # Q# реализация
│ └── qiskit_sim.py # Qiskit реализация
├── visualization/
│ ├── __init__.py
│ ├── terminal.py # Терминальный вывод
│ └── led_control.py # Управление LED-лентой
└── requirements.txt |
|
Вот законченное основное приложение, объединяющее все элементы:
| Python | 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
| #!/usr/bin/env python3
import argparse
import os
from typing import Tuple, List
from abc import ABC, abstractmethod
# Абстрактный базовый класс для квантовых симуляторов
class QuantumSimulator(ABC):
@abstractmethod
def run_simulation(self, num_positions: int) -> str:
"""Запустить квантовую симуляцию и вернуть бинарную строку результатов"""
pass
# Реализация для Qiskit
class QiskitSimulator(QuantumSimulator):
def run_simulation(self, num_positions: int) -> str:
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister
from qiskit.providers.aer import AerSimulator
qubits_needed = num_positions * 3
qr = QuantumRegister(qubits_needed, 'q')
cr = ClassicalRegister(qubits_needed, 'c')
circuit = QuantumCircuit(qr, cr)
# Построение квантовой схемы (весь код из предыдущих разделов)
# ...
# Запуск симуляции
simulator = AerSimulator()
result = simulator.run(circuit).result()
counts = result.get_counts(circuit)
return list(counts.keys())[0]
# Реализация для Q#
class QSharpSimulator(QuantumSimulator):
def __init__(self, source_code: str):
import qsharp
self.source_code = source_code
qsharp.eval(self.source_code)
def run_simulation(self, num_positions: int) -> str:
import qsharp
result = qsharp.run(
f"QuantumDecoration.CreateQuantumDecoration({num_positions})",
shots=1
)
return ''.join(['1' if x == qsharp.Result.One else '0' for x in result[0]])
# Функции обработки и визуализации (из предыдущих разделов)
# ...
def main():
parser = argparse.ArgumentParser(description='Квантовая новогодняя елка')
parser.add_argument('--height', type=int, default=12, help='Высота елки')
parser.add_argument('--mode', choices=['terminal', 'led'], default='terminal',
help='Режим вывода: терминал или LED-лента')
parser.add_argument('--backend', choices=['qsharp', 'qiskit'], default='qsharp',
help='Квантовый бэкенд: Q# или Qiskit')
args = parser.parse_args()
# Выбор симулятора
if args.backend == 'qsharp':
try:
with open('tree.qs', 'r') as file:
qs_content = file.read()
simulator = QSharpSimulator(qs_content)
except FileNotFoundError:
print("Q# источник не найден, использую Qiskit")
simulator = QiskitSimulator()
else:
simulator = QiskitSimulator()
# Выбор визуализатора
if args.mode == 'terminal':
draw_christmas_tree(args.height, simulator)
else:
setup_led_strip()
apply_quantum_decorations_to_physical_tree(args.height, simulator)
if __name__ == "__main__":
main() |
|
| Bash | 1
| python main.py --height 15 --backend qiskit --mode terminal |
|
В результате получилось компактное, но мощное приложение, демонстрирующее применение квантовых вычислений в неожиданном контексте праздничных украшений. Каждый запуск создает уникальную елку, отражающую квантовые феномены, что делает ее не просто игрушкой, а настоящим наглядным пособием по квантовой механике.
Нарисовать новогоднюю ёлку в паскале.
Графика в паскале.Создать новогоднюю ёлку в паскале из 3 треугольников. с игрушками на ёлке Нарисовать новогоднюю ёлку (с игрушками) из 3 треугольников
Создать новогоднюю ёлку в паскале из 3 треугольников. с игрушками на ёлке Конкурс на новогоднюю елку 2015
В прошлом году был конкурс на самую прикольную елку.
Предлагаю повторить:) Написать программу, рисующую новогоднюю ёлку
Здравствуйте помогите мне пожалуйста написать программу чтоб она рисовала новогоднею ёлку Построить рисунок, изображающий новогоднюю ёлку
1. Построить рисунок, изображающий новогоднюю ёлку. UMI Как на название раздела поместить "новогоднюю шапочку"
Поддерживаю сайт на UMI CMS. Поступило задание - на название одного из разделов на первую букву... Создать на новогоднюю тему какую-нибудь картинку
Здраствуйте ! Помогите пожалуеста создать рисунок на паскале на новогоднюю тему 2014 года . Года... Всем добрый вечер. Мне нужно создать Новогоднюю анимационную открытку на Делфи
Мне нужно срочно создать Новогоднюю анимационную открытку на Делфи. У кого есть какие-то исходники... Создать простую новогоднюю открытку
На новогодней открытки должна быть елка,снеговик и надпись с новым годом. Как и чем можно украсить программу свою?
Я бы хотел узнать как программисты и чем вообще украшают свои программы,так как я новичок мало что... Как украсить консольное приложение Win32?
Мне надо "украсить" консольную программу Win32, но как я не знаю!!! Подскажите пожалуйста!!!! Как украсить форму в делфи
Всем привет. Скажите пожалуйста как можно украсить форму, кнопки, ДБГрид, комбобокс, едиты,...
|




